Numerical Analysis

Back

Newton Raphson Method (Theoretical and Programmatic Approach)

How Newton Raphson is useful in root optimisation?

This is important topic to discuss here. So, let’s get some intution about it.

Try to Visualize few points from the graph below

General Formula is given by:

The descriptive algorithm is as follows:

1. Start

2. Input Equation

3. Find Range and initialize (a = min_range, b = max_range)

4. repeat
  {
    compute root r according to formula
  }

General Description:

1. So, the newton raphson methods determines the root approximation according to formula.

2. This process is repeated likewise till the iterations we match or from the error analysis.

Graphical Intution:

Root Analysis through Iterations

Equation:

Range Obtained from the previous understanding:

(a,b) = (0,1)

Root Analysis:

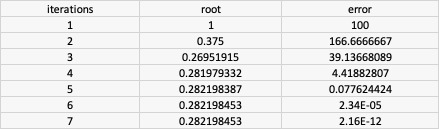
Snippets that support MATLAB/ OCTAVE and Python3

MATLAB SCRIPT

clc;
close all;
clear all;
f = @(x) exp(x) - x - 2;
fd = @(x) exp(x) - 1;
root(1) = 2;
for n = 2:30
    root(n) = (root(n-1) - f(root(n-1)/fd(root(n-1));
    if n>1
    p = root(n);
    q = root(n-1);
    er(n) = abs((p - q)/p)*100;
    disp('Percentage Error is ');
    disp(er(n));
    if(er(n)<(1/10^(6-1)))
    disp(root(n));
    break;
    end
    end
end
iterations = n;
i = 1:iterations;
er = er';
i = i';
root = root';
t = table(i,root,er)

Python3 SCRIPT

# Python3 Script for Newton Raphson Method


def f(x):
    
    return x**2 - x - 2

def fd(x):
    
    return 2*x - 1

max_range = 4
root = []
er = []
n =1
root.append(max_range)
er.append(100)
while(1):
    root.append(root(n-1) - f(root(n-1))/fd(root(n-1))    
    if n>0:
        p = root[n]
        q = root[n-1]
        er.append(abs((p - q)/p)*100)
        print('Percentage Error is ')
        print(er[n])
        if(er[n]<(1/10**(4-1))):
            print(root[n])
            print(n+1)
            break
    n=n+1;